Pergeseran (Translasi) Matematika Khusus Kelas 9
Pergeseran (Translasi) Matematika Khusus Kelas 9 - Translasi adalah proses memindahkan semua titik suatu bangun dengan jarak dan arah yang sama. Sebenarnya translasi matematika cukup mudah jika kita sudah paham dengan baik dasar berpikirnya. Untuk memahami tranlasi dengan baik kita bisa memulai dari mengindetifikasi kegiatan sehari-hari yang termasuk dalam kategori translasi.
Pergeseran (Translasi) Matematika Khusus Kelas 9
Pernahkah kamu menggeser meja dari satu tempat ke tempat lainnya? Ketika kamu berhasil memindahkan meja tersebut maka posisi meja akan berubah dari posisi awal menuju posisi akhir. Gerakan memindahkan meja tersebut merupakan salah satu contoh dari translasi.
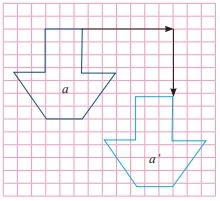
Perhatikan bangun datar a pada gambar di atas. Kemudian perhatikan bangun a' yang merupakan bayangan dari a. Kamu dapat memperoleh bangun datar a' dengan cara menggeser (mentranslasikan) bangun a.
Untuk mengetahui jenis translasi yang menggerakkan bangun a sehingga menjadi bangun a', ikuti langkah-langkah berikut ini.
- Pilih sebarang titik sudut pada bangun awal a (kamu dapat memilih sebarang titik sudut dari bangun), kemudian beri nama titik sudut tersebut A. Pada titik sudut bayangan yang bersesuaian dengan titik A berikan nama A'.
- Dari titik A gambarlah garis horizontal sampai tepat berada pada bagian atas titik A'. Selanjutnya gambarlah garis vertikal dari titik tersebut sehingga garis tersebut bertemu dengan titik A'.
- Hitung berapa satuan panjang garis horizontal yang menunjukkan seberapa jauh bangun datar a bergeser (bertranslasi) secara horizontal (ke kanan).
- Hitung berapa satuan panjang garis vertikal yang menunjukkan seberapa jauh bangun datar a bergeser (bertranslasi) secara vertikal (ke bawah).
Jika suatu translasi (pergeseran) pada suatu benda dilakukan sepanjang garis horizontal, maka translasi tersebut akan bernilai positif jika benda ditranslasikan ke arah kanan, dan bernilai negatif jika benda ditranslasikan ke arah kiri.
Jika suatu translasi (pergeseran) pada suatu benda dilakukan sepanjang garis vertikal, maka translasi tersebut akan bernilai positif jika benda ditranslasikan ke arah atas, dan bernilai negatif jika benda ditranslasikan ke arah bawah.
Translasi adalah salah satu jenis transformasi yang bertujuan untuk memindahkan semua titik suatu bangun dengan jarak dan arah yang sama.
Translasi pada bidang Kartesius dapat dilukis jika kamu mengetahui arah dan
seberapa jauh gambar bergerak secara mendatar dan atau vertikal. Untuk nilai yang
sudah ditentukan a dan b yakni translasi memindah setiap titik P (x, y) dari
sebuah bangun pada bidang datar ke P’ (x + a, y + b). Translasi dapat disimbolkan
dengan (x, y) → (x + a, y + b)
Cara lain untuk menentukan translasi adalah dengan menunjukkan pencerminan terhadap dua garis sejajar, kemudian mencerminkan gambar/bangun terhadap garis lain yang sejajar. Jika belum memahami pencerminan bisa dipelajari di Pencerminan (Refleksi) Khusus Kelas 9.
Untuk memudahkan anda belajar trnslasi berikut ini rumus umum untuk tranlasi.
Perhatikan contoh berikut ini.
Contoh
Perhatikan gambar di bawah.
Garis m dan n sejajar. Tentukan apakah bangun berwarna merah merupakan translasi bangun yang berwarna biru, segi empat ABCD.
Penyelesaian
Cerminkan segi empat ABCD di garis m. Hasilnya yaitu bangun berwarna hijau, segi empat A'B'C'D'. Kemudian cerminkan bangun berwarna hijau, segi empat AA'B'C'D' di garis n menghasilkan segi empat berwarna merah. Segiemmpat berwarna merah, A''B''C''D'' memiliki bentuk dan arah yang sama dengan segi empat ABCD.
Jadi, segi empat A''B''C''D'' merupakan bayangan hasil translasi segi empat ABCD.
Contoh
Gambar di atas menunjukkan segitiga ABC yang ditranslasikan 4 satuan ke kanan dan 3 satuan ke bawah. Hal ini dapat dinyatakan sebagai (x, y) → (x + 4, y – 3). Koordinat bayangan hasil translasinya sebagai berikut
A (–3, 1) → A' (–3 + 4, 1 – 3) atau A' (1, –2)
B (–1, 4) → B'(–1 + 4, 4 – 3) atau B' (3, 1)
C (–2, –1) → C' (–2 + 4, –1 – 3) atau C' (2, –4)
Jadi bisa kita simpulkan :
Jika suatu translasi pada suatu titik dilakukan sepanjang garis horizontal, maka bilangan translasi tersebut akan bernilai positif jika titik tersebut ditranslasikan ke arah kanan, dan bernilai negatif jika titik ditranslasikan ke arah kiri. Jika translasi pada suatu titik dilakukan sepanjang garis vertikal, maka bilangan translasi tersebut akan bernilai positif jika titik ditranslasikan ke arah atas, dan bernilai negatif jika titik ditranslasikan ke arah bawah.
 Matematika Khusus Kelas 9){kind=link}