Perputaran (Rotasi) Matematika Khusus Kelas 9 - Kali ini kita akan membahas tentang perputaran atau rotasi yang merupakan salah satu jenis transformasi. Sebelumnya kita sudah membahas pencerminan (refleksi) dan pergeseran (translasi) yang juga merupakan bagian dari jenis transformasi dalam matematika.
Perputaran (Rotasi) Matematika Khusus Kelas 9
Rotasi matematika adalah salah
satu bentuk transformasi yang memutar setiap titik pada gambar sampai sudut dan
arah tertentu terhadap titik yang tetap. Titik tetap ini disebut pusat rotasi.
Besarnya sudut dari bayangan benda terhadap posisi awal disebut dengan sudut
rotasi.
Beberapa benda dapat berotasi dengan pusat rotasi berada di dalam benda itu sendiri. Salah satu contohnya adalah Planet Bumi berputar atau berotasi pada porosnya. Pada pembelajaran terdahulu, kamu juga telah mempelajari bahwa beberapa benda memiliki simetri putar. Jika suatu bangun/gambar dapat dirotasikan kurang dari 360o terhadap titik pusat rotasi sedemikian sehingga bayangan dan gambar awalnya sama, maka bangun/gambar tersebut memiliki simetri putar.
Gambar di atas menunjukkan segi enam beraturan yang memiliki 6 bentuk yang sama jika diputar/dirotasikan. Karena segi enam setelah diputar kurang dari 360o (termasuk 0o ) bentuknya sama seperti semula, maka segi enam memiliki simetri putar tingkat enam.
Jika suatu bangun setelah diputar satu putaran pada pusatnya dan bentuknya sama sepeti gambar awal setelah n putaran, maka bangun tersebut memiliki simetri putar tingkat n, untuk n > 1.
Rotasi merupakan salah satu bentuk transformasi dalam matematika yang memutar
setiap titik pada gambar sampai sudut dan arah tertentu terhadap titik yang
tetap. Titik tetap ini disebut pusat rotasi. Besarnya sudut dari bayangan benda
terhadap posisi awal disebut dengan sudut rotasi.
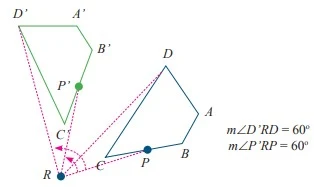
Gambar di bawah ini menunjukkan rotasi bangun ABCD terhadap pusat rotasi, R. Besar sudut ARA’, BRB’, CRC’, dan DRD’ sama. Sebarang titik P pada bangun ABCD memiliki bayangan P’ di A’B’C’D’ sedemikian sehingga besar ∠PRP’ konstan. Sudut ini disebut sudut rotasi.
Suatu rotasi ditentukan oleh arah rotasi. Jika berlawanan
arah dengan arah perputaran jarum jam, maka sudut putarnya positif. Jika searah
perputaran jarum jam, maka sudut putarnya negatif. Pada rotasi, bangun awal
selalu kongruen dengan bayangannya.
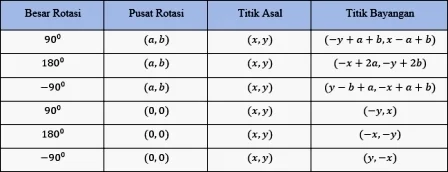
Untuk memudahkan memahami materi perputaran (rotasi) matematika khusus kelas 9, berikut ini tabel rumus rotasi khusus untuk tingkatan SMP kelas 9.
Contoh
1. Tentukan bayangan segitiga JKL dengan koordinat J (1, 2), K
(4, 2), dan L (1, –3) pada rotasi 90o berlawanan jarum jam dengan
pusat rotasi adalah titik L.
Penyelesaian:
Koordinat bayangannya J’ (–4, –3), K’ (–4, 0), dan L’ (1,
–3).
2. Tentukan bayangan trapesium WXYZ dengan koordinat W (–4, 2),
X (–3, 4), Y (–1, 4) dan Z (–1, 2) pada rotasi 180o dengan pusat
rotasi O (0, 0).
Penyelesaian:
Koordinat bayangannya W’ (4, –2), X’ (3, –4), Y’ (1, –4) dan Z’ (1, –2).