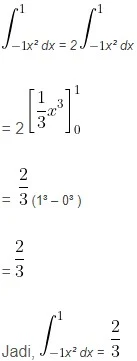Teorema Dasar Kalkulus, Contoh Soal
Teorema Dasar Kalkulus, Contoh Soal – Sebelum kita masuk ke penjelasan tentang Teorema Dasar Kalkulus, terlebih dahulu admin akan membagikan bagaimana awal mula Teorema Dasar Kalkulus digunakan. Dulu, untuk menyelesaikan persamaan integral tentu orang-orang menggunakan sebuah cara yang disebut dengan Jumlah Riemann. Setelah bertahun – tahun kemudian, para ilmuwan seperti Newton dan Leibniz mengaji lebih dalam mengenai kemiringan garis singgung dan luas daerah kurva. Mereka memahami dan memanfaatkan hubungan antara anti-turunan dengan integral tentu. Hubungan inilah yang disebut dengan Teorema Dasar Kalkulus Pertama.
Teorema dasar kalkulus menjelaskan tentang hubungan antara dua operasi pusat kalkulus , yaitu diferensiasi dan integrasi. Sesungguhnya diferensiasi dengan integrasi merupakan dua opeasi inverse seperti penjumlahan dengan pengurangan atau pembagian dengan perkalian. Teorema Dasar Kalkulus digunakan untuk membantu menyelesaikan proses pengintegralan suatu fungsi. Teorema dasar kalkulus ada dua, pertama disebut dengan Teorema Dasar Kalkulus I dan yang kedua disebut dengan Teorema Dasar Kalkulus II. [ Pertidaksamaan Eksponen, Contoh Soal Eksponen ]
Teorema Dasar Kalkulus
Berdasarkan definisi integral tertentu, maka dapat diturunkan suatu teorema yang disebut dengan Teorema Dasar Kalkulus.
Jika f kontinu pada interval [a, b] , dan andaikan F sembarang antiturunan dari f pada interval tersebut, maka
Dalam pengerjaan hitung integral tertentu ini akan lebih mudah jika kalian menggunakan teorema-teorema berikut.
Teorema 1
Kelinearan
Jika f dan g terintegralkan pada interval [a, b] dan k suatu konstanta, maka
Teorema 2
Perubahan batas
Jika f terintegralkan pada interval [a, b] maka:
Teorema 3
Teorema penambahan interval
Jika f terintegralkan pada suatu interval yang memuat tiga titik a, b, dan c, maka
Teorema 4
Contoh Soal
1. Tentukan 
Jawab:
Oleh karena untuk f(x) = x², berlaku f( -x) = f(x), maka f(x) = x² merupakan fungsi genap. Dengan menggunakan Teorema 4, akan diperoleh:
2. Hitunglah 
Jawab:
= -1/3 ( cos π/2 – cos 0 ) + ( sin π/6 sin 0 )
= -1/3 . (-1) + ½
= 5/6
Jadi, = 5/6
